Key Findings and Discussion

The Congressional members of the Census Monitoring Board examined the results of the 1990 PES, the model for next year’s Accuracy and Coverage Evaluation (ACE), to predict the effectiveness of the ACE in correcting local undercounts. The Board examined the 5,170 block clusters surveyed in the 1990 PES. For a detailed description of the analysis, see Section IV: Methodology and Section V: Limitations.

Areas with undercounts greater than two percent would have received small additions: an average increase of only 1.36 percent in 2,200 clusters where the PES indicated there should have been an average increase of 8.97 percent to remedy the undercounts.
Areas with accurate counts (within two percent of a full count) would have received small additions: an average increase of 0.6 percent in 1,591 clusters.
Most areas with overcounts also would have received small additions: an average increase of 0.17 percent in 996 clusters with overcounts between two and 10 percent, where the PES indicated there should have been an average decrease of 4.89 percent to remedy the overcounts.

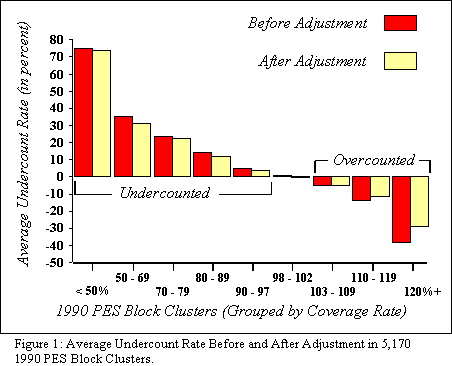
The dark bars in Figure 1 show the undercount rates measured by the PES and the light bars show the undercounts remaining after statistical adjustment. If statistical adjustment had succeeded, the light bars would be much smaller than the dark bars. Instead, however, the two sets of bars are almost identical. Where the survey measured large undercounts, statistical adjustment tended to make just a small improvement. Where the survey measured overcounts, statistical adjustment also tended to make only small improvements – or to increase overcounts.

1. STATISTICAL ADJUSTMENT CANNOT CORRECT LARGE UNDERCOUNTS IN LOCAL AREAS.
Analysis of the 1990 PES adjustments reveals that statistical adjustment is insensitive to local undercount rates. The Bureau’s adjustment would have added people marginally to undercounted areas and to many overcounted areas, instead of adding large numbers to areas with large undercounts, and lowering numbers from areas with overcounts. This approach is inadequate to overcome the unfair under-representation of heavily undercounted neighborhoods (Figure 2).

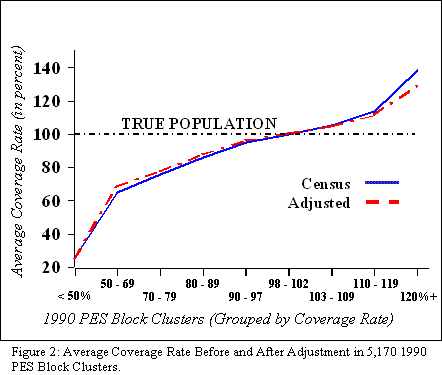
If statistical adjustment succeeded, the line in Figure 2 representing adjusted coverage rates would be very similar to the horizontal line labeled “True Population.” Instead, the line representing the adjusted coverage rates is almost identical to the line representing the census coverage rates.

Unfortunately, the insensitivity to local undercount rates is not unique to the 1990 PES. Any use of “synthetic estimation” to distribute undercount over a large region will likely have the same result – it will not correct large undercounts in local areas.

Poststratification Fails: By design, statistical adjustment using synthetic estimation does not correct extreme errors – large undercounts in certain minority areas, for example. This design depends on a false assumption, the homogeneity assumption: that people meeting certain demographic criteria have the same probability of being counted in the census, regardless of where they live in a region.

To try to satisfy the homogeneity assumption, the Bureau categorizes all people in each region by criteria such as age, race, gender, and tenure. Each combination of these categories forms a demographic poststratum. Poststrata cut across all the blocks in a region (that is, each block is divided into several poststrata, and each poststratum contains people from many blocks across a broad region). The Bureau multiplies the count of all members of a poststratum in each block by a common adjustment factor.

For example, in 1990, African American women between 18 and 29 paying rent in cities in a particular region formed one poststratum. In each block, each woman in that poststratum was multiplied by an adjustment factor. The same factor was used for that poststratum in every block in the entire region. An adjustment factor was applied to each person in each poststratum in each region. The adjusted poststrata totals in each block were summed, to determine adjusted population in each block.

The logic is that the census misses similar people at similar rates, so a common adjustment factor applied to people fitting a certain description should correct large undercounts. A high adjustment factor for the young, urban African American women in the example above is intended to make large additions to areas where many women fitting that description live.

However, real-life examples confound this logic. For example, African-American women renting in Chicago’s affluent “Gold Coast” are not undercounted at the same rate as African American women renting a few miles away, in or around the Robert Taylor Homes public housing project.

If statistical adjustment in poststrata worked, one would expect to see many people added to areas where many people were missed. This did not occur.

Instead, heavily undercounted local areas surveyed in the 1990 PES would have received only marginal increases, on average (Figure 3). Correlation analysis shows that poststratification and synthetic estimation, as applied in the 1990 PES and planned for the 2000 ACE, are ineffectual in correcting large local undercounts. In the 1990 PES block clusters, there was practically no correlation between the size of the directly estimated undercount and the size of the proposed adjustment using synthetic estimation. The computed correlation was 0.097. If adjustment were effective, we would expect the correlation to be much stronger.

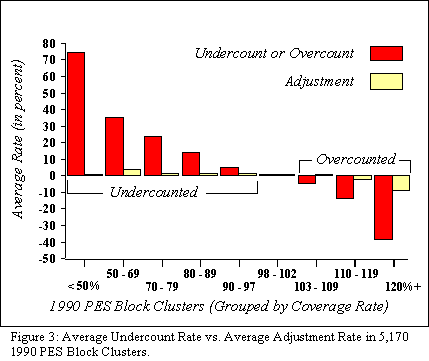
In Figure 3, the two sets of bars would be very similar if statistical adjustment did a good job of correcting for the undercounts and overcounts measured by the PES. But the two sets of bars are radically different. The bars representing statistical adjustment are much smaller, indicating that statistical adjustment corrects only a negligible portion of the apparent net undercount measured by the PES. In fact, the bars representing statistical adjustment are all just about the same size. One bar, representing the average adjustment in 996 clusters with census overcounts between two and 10 percent, even points in the wrong direction: population is increased even where overcounts were measured.

Minority Neighborhoods Disproportionately Affected:The evidence clearly indicates that statistical adjustment will not correct large undercounts or overcounts in small areas such as blocks and neighborhoods. Heavily undercounted areas will remain heavily undercounted. Overcounts in many areas will be increased. Until the actual enumeration of people in the census is improved in heavily undercounted local areas, the differential undercount will persist at the local level.

A Case in Point: Robert Taylor Homes
Robert Taylor Homes is the picture of a hard-to-count neighborhood: low-income residents in a dense urban area who do not trust government. Covering 15 city blocks in Chicago, Robert Taylor has 22 sixteen-story buildings. Ninety-nine percent of the residents are African American. Eighty-four percent earn less than $10,000 a year.

After the 1990 census, Chicago Housing Authority records showed the census missed 3,500 people in Robert Taylor – a local undercount of 29 percent.⁴ Statistical adjustment would have added 673 – only a five percent increase, leaving one out of four Robert Taylor residents (counted by the Chicago Housing Authority) uncounted by the census.

Statistical adjustment would have added over 100,000 people to Illinois. But only 673 would have been added where they were needed most – in the 15 blocks of Robert Taylor Homes. While Illinois would have supposedly shown little or no undercount after adjustment, one in four Robert Taylor residents would have remained uncounted and without their fair share of representation or funding.
A 2nd Case in Point: Lincolnwood and Bronzeville
The 1990 PES surveyed block clusters in Lincolnwood and Bronzeville, two Chicago neighborhoods. The cluster surveyed in Bronzeville was heavily undercounted by about 17 percent. The cluster surveyed in Lincolnwood was heavily overcounted by about 29 percent. Yet statistical adjustment would have added people to the neighborhoods surrounding both surveyed clusters. According to the Bureau’s official figures, statistical adjustment would have added only 4.4 percent to the neighborhood surrounding the heavily undercounted Bronzeville cluster. Statistical adjustment would have added 1.1 percent to the neighborhood surrounding the heavily overcounted Lincolnwood cluster⁵ (see map).

In a nation as large, diverse and mobile as ours, some people will be missed. That is unavoidable. But statistical adjustment consistently misses the same people in the same communities – the very communities that depend on the census for the health care, schools and child care that come with being counted. The solution is to actually count people better, not to rely upon a statistical adjustment incapable of correcting the problem.

2. STATISTICAL ADJUSTMENT WILL ADD PEOPLE TO MANY OVERCOUNTED AREAS.
In the 1990 PES block clusters, 1,379 (out of 5,170) were overcounted.⁶ The PES indicated the population as reported in these areas should have been reduced by an average of 8.9 percent. However, statistical adjustment would have only reduced the population by an average of one (1.0) percent. In addition, the majority of overcounted PES block clusters (996) would have received an average increase of 0.17 percent (Figure 1).

Credibility Gap: Local leaders (such as city council members, mayors, city planners, social service providers, school boards, county commissioners, etc.) who expect substantial gains in representation and funding through statistical adjustment are likely to be disappointed. The data show that blocks and neighborhoods will experience only marginal change, regardless of the severity of their undercount or overcount (Figure 3).

On average, statistical adjustment marginally reduces undercounts in undercounted blocks. In addition, statistical adjustment adds to overcounts in many overcounted blocks. Statistical adjustment does not alleviate the essential unfairness to heavily undercounted communities. By asserting the adjustment will correct undercounts in 2000, proponents of statistical adjustment have raised unrealistic expectations likely to create a “credibility gap” that may compromise future census efforts and condemn future generations to continued undercounts.

Director of the Census Bureau, Dr. Kenneth Prewitt said, “I don`t want to create a census in 2000 that creates a problem for 2010. We could over promise and then come in 2010 and the communities will say, ‘My God, you told us that if we filled this form out, we were going get a new school, so where is it?’”⁷

A Case in Point: Sacramento City Council Districts

Sacramento City Council member Lauren Hammond testified that the severe undercount in her district – a predominantly African American area – resulted in insufficient resources for a much-needed middle school: “I have four high schools and eight elementary schools and not one darn middle school because there aren`t the numbers to reflect that.”⁸

Logic and school enrollment suggest Councilwoman Hammond’s district needs a middle school. She believes statistical adjustment will help get one. The evidence suggests that it won’t.

Marginal increases in the population of heavily undercounted blocks in the Councilwoman’s district would be unlikely to strengthen her case for a middle school. In fact, her argument might be weakened, since increases in her district would be offset by comparable increases to undercounted and overcounted blocks in neighboring districts.

Aggregation of adjustments at higher levels of geography (big cities, states), is likely to produce a harmful result: Councilwoman Hammond’s reports of egregious undercounts in her district would be contradicted by the appearance of only minor undercounts in Sacramento, California and the nation. Legitimate complaints about census undercount would be precluded by the notion that the undercount had been officially eliminated. Adjustment can appear to substantially reduce the undercount at the big-city and state level, without correcting undercounts in local areas.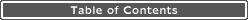